1209: 【例】【基础】经典递归问题——汉诺塔

内存限制：16 MB 时间限制：1.000 S
评测方式：文本比较 命题人：
提交：28 解决：17

题目描述

汉诺塔（又称河内塔）问题是印度的一个古老的传说。开天辟地的神勃拉玛在一个庙里留下了三根金刚石的棒，第一根上面套着64个圆的金片，最大的一个在底下，其余一个比一个小，依次叠上去，庙里的众僧不倦地把它们一个个地从这根棒搬到另一根棒上，规定可利用中间的一根棒作为帮助，但每次只能搬一个，而且大的不能放在小的上面。

面对庞大的数字(移动圆片的次数)18446744073709551615，看来，众僧们耗尽毕生精力也不可能完成金片的移动。 

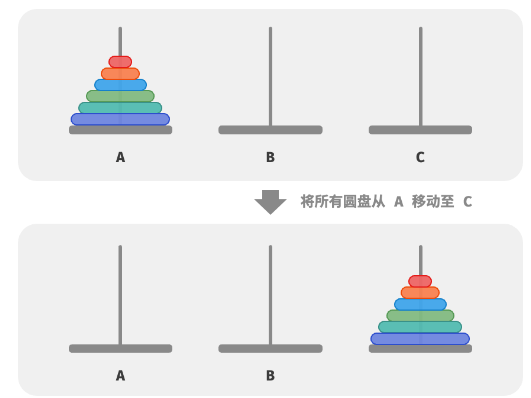
后来，这个传说就演变为汉诺塔游戏:

1.有三根杆子A,B,C。A杆上有若干碟子

2.每次移动一块碟子,小的只能叠在大的上面

3.把所有碟子从A杆全部移到C杆上

经过研究发现，汉诺塔的破解很简单，就是按照移动规则向一个方向移动金片：  

如3阶汉诺塔的移动：A→C,A→B,C→B,A→C,B→A,B→C,A→C   

此外，汉诺塔问题也是程序设计中的经典递归问题。

算法思路：

1.如果只有一个金片，则把该金片从源移动到目标棒，结束。

2.如果有n个金片，则把前n-1个金片移动到辅助的棒，然后把自己移动到目标棒，最后再把前n-1个移动到目标棒.

输入

一个整数N，表示A柱上有N个碟子。（0<n<=10）

输出

若干行，即移动的最少步骤

样例输入 复制 

3

样例输出 复制 

A To C
A To B
C To B
A To C
B To A
B To C
A To C

提示

二．抽象为数学问题：

  如下图所示，从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数

当 n = 1 时（只有一个盘子）

  • • 第1步：直接将1号盘子从A柱移动到C柱。总移动次数 = 1 次

当 n = 2 时（有两个盘子）

  • • 第1步：将1号盘子（较小的）从A柱移动到B柱。

  • • 第2步：将2号盘子（较大的）从A柱移动到C柱。

  • • 第3步：将1号盘子从B柱移动到C柱上2号盘子之上。总移动次数 = 3 次

当 n = 3 时（有三个盘子）

  • • 第1步：将1号盘子从A柱移动到C柱。

  • • 第2步：将2号盘子从A柱移动到B柱。

  • • 第3步：将1号盘子从C柱移动到B柱，放在2号盘子上。

  • • 第4步：将3号盘子（最大的）从A柱移动到C柱。

  • • 第5步：将1号盘子从B柱移动到A柱。

  • • 第6步：将2号盘子从B柱移动到C柱，放在3号盘子上。

  • • 第7步：将1号盘子从A柱移动到C柱，放在所有盘子上。总移动次数 = 7 次

观察规律

通过观察上述几个例子，我们可以发现，每当盘子数量增加1时，移动次数就会翻倍并加1。这是因为要移动n个盘子到目标柱子，我们首先需要移动上面的n-1个盘子到辅助柱子，然后移动最大的盘子到目标柱子，最后再将那n-1个盘子从辅助柱子移动到目标柱子上。因此，对于n个盘子的情况，总移动次数符合以下规律：

  • • 对于1个盘子： 次

  • • 对于2个盘子： 次

  • • 对于3个盘子： 次

  • • 以此类推，对于n个盘子，总移动次数为：2n - 1次

调用方法的栈机制:（特点：先进后出）

       从主线程开始调用方法（函数）进行不停的压栈和出栈操作，函数的调用就是将函数压如栈中，函数的结束就是函数出栈的过程，这样就保证了方法调用的顺序流，即当函数出现多层嵌套时，需要从外到内一层层把函数压入栈中，最后栈顶的函数先执行结束（最内层的函数先执行结束）后出栈，再倒数第二层的函数执行结束出栈，到最后，第一个进栈的函数调用结束后从栈中弹出回到主线程，并且结束。

算法分析（递归算法）：

       我们在利用计算机求汉诺塔问题时，必不可少的一步是对整个实现求解进行算法分析。到目前为止，求解汉诺塔问题最简单的算法还是同过递归来求，至于是什么是递归，递归实现的机制是什么，我们说的简单点就是自己是一个方法或者说是函数，但是在自己这个函数里有调用自己这个函数的语句，而这个调用怎么才能调用结束呢？，这里还必须有一个结束点，或者具体的说是在调用到某一次后函数能返回一个确定的值，接着倒数第二个就能返回一个确定的值，一直到第一次调用的这个函数能返回一个确定的值。

实现这个算法可以简单分为三个步骤：

（1）     把n-1个盘子由A 移到 B；

（2）     把第n个盘子由 A移到 C；

（3）     把n-1个盘子由B 移到 C；

我们不难发现，移到的步数必定为奇数步：

（1）中间的一步是把最大的一个盘子由A移到C上去；

（2）中间一步之上可以看成把A上n-1个盘子通过借助辅助塔（C塔）移到了B上，

（3）中间一步之下可以看成把B上n-1个盘子通过借助辅助塔（A塔）移到了C上； 


#include <iostream>
using namespace std;

// 移动汉诺塔盘子的函数，n是盘子数量，src是起始柱子，aux是辅助柱子，dest是目标柱子
void hanoi(int n, char src, char aux, char dest) {
    if (n == 1) { // 递归终止条件
        cout <<  src << " To " << dest << endl;
        return;
    }
    // 移动上面 n-1 个盘子到辅助柱子
    hanoi(n-1, src, dest, aux);
    // 移动最底下的盘子到目标柱子
    cout << src << " To " << dest << endl;
    // 将辅助柱子上的盘子移动到目标柱子
    hanoi(n-1, aux, src, dest);
}

int main() {
    int n; // 盘子数量
    cin >> n;
    // 调用汉诺塔函数，假设初始时所有盘子都在 'A' 柱子上，目标是移动到 'C' 柱子，'B' 作为辅助柱子
    hanoi(n, 'A', 'B', 'C');
    return 0;
}

来源/分类

提交提交记录统计露一手!