1327: 【入门】费马定理

内存限制：16 MB 时间限制：1.000 S
评测方式：文本比较 命题人：
提交：16 解决：12

题目描述

公元1640年，法国著名数学家费马发现：

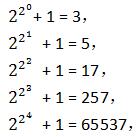
而3、5、17、257、65537都是质数，于是费马猜想：对于一切自然数n，2n+1都是质数，可是到了1732年，数学家欧拉发现一个数n并不满足费马的这个猜想，请问欧拉发现的这个数n最小是多少？（在long long的范围内）（7.2）

输入

无

输出

满足条件的数n

样例输入 复制

样例输出 复制

提示

ans=2
t1=2
t2=0
while True:
    t1*=2
    t2=int(2**t1)+1
    flag=0
#2不可能是2的n次方+1的因数，可以直接从3开始的奇数开始判断i是否是素数
    for i in range(3,int(t2**0.5)+1,2):  
        if (t2%i==0):
            print(ans)
            flag=1
            break
    if (flag==1):
        break
    ans+=1

来源/分类

提交提交记录统计露一手!