2401: 【例】【普及-】【P1563】玩具谜题
题目描述
小南有一套可爱的玩具小人, 它们各有不同的职业。
有一天, 这些玩具小人把小南的眼镜藏了起来。 小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图:
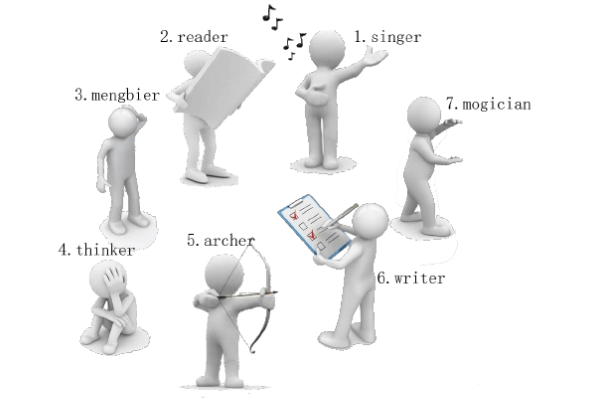
这时 singer 告诉小南一个谜題: “眼镜藏在我左数第 个玩具小人的右数第 个玩具小人的左数第 个玩具小人那里。 ”
小南发现, 这个谜题中玩具小人的朝向非常关键, 因为朝内和朝外的玩具小人的左右方向是相反的: 面朝圈内的玩具小人, 它的左边是顺时针方向, 右边是逆时针方向; 而面向圈外的玩具小人, 它的左边是逆时针方向, 右边是顺时针方向。
小南一边艰难地辨认着玩具小人, 一边数着:
singer 朝内, 左数第 个是 archer。
archer 朝外,右数第 个是 thinker 。
thinker 朝外, 左数第 个是 writer。
所以眼镜藏在 writer 这里!
虽然成功找回了眼镜, 但小南并没有放心。 如果下次有更多的玩具小人藏他的眼镜, 或是谜题的长度更长, 他可能就无法找到眼镜了。所以小南希望你写程序帮他解决类似的谜题。 这样的谜題具体可以描述为:
有 个玩具小人围成一圈, 已知它们的职业和朝向。现在第 个玩具小人告诉小南一个包含 条指令的谜題, 其中第 条指令形如“左数/右数第 ,个玩具小人”。 你需要输出依次数完这些指令后,到达的玩具小人的职业。
输入
输入的第一行包含两个正整数 ,表示玩具小人的个数和指令的条数。
接下来 行,每行包含一个整数和一个字符串,以逆时针为顺序给出每个玩具小人的朝向和职业。其中 表示朝向圈内, 表示朝向圈外。 保证不会出现其他的数。字符串长度不超过 且仅由小写字母构成,字符串不为空,并且字符串两两不同。整数和字符串之间用一个空格隔开。
接下来 行,其中第 行包含两个整数 ,表示第 条指令。若 ,表示向左数 个人;若 ,表示向右数 个人。 保证 不会出现其他的数,。
输出
样例输入 复制
7 3
0 singer
0 reader
0 mengbier
1 thinker
1 archer
0 writer
1 mogician
0 3
1 1
0 2样例输出 复制
writer提示
【样例1说明】
这组数据就是【题目描述】 中提到的例子。
【子任务】
子任务会给出部分测试数据的特点。 如果你在解决题目中遇到了困难, 可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表:
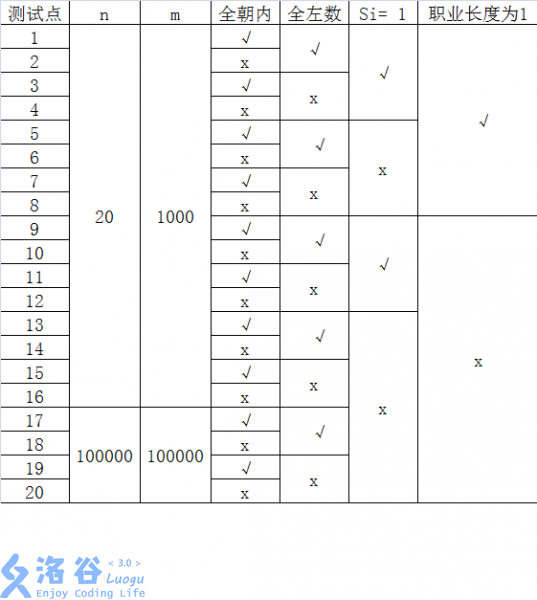
其中一些简写的列意义如下:
-
全朝内: 若为“√”, 表示该测试点保证所有的玩具小人都朝向圈内;
-
全左数:若为“√”,表示该测试点保证所有的指令都向左数,即对任意的 ;
-
:若为“√”,表示该测试点保证所有的指令都只数 个,即对任意的 ;
职业长度为 :若为“√”,表示该测试点保证所有玩具小人的职业一定是一个长度为的字符串。
分析:
如果模拟现实中击鼓传花的过程,一个传一个,模拟礼物在谁的手上,考虑到数据范围很大,两重循环的做法会超时。把手里拥有礼物的第一个同学称为0号同学(因为数组习惯从0开始,最后一名同学是 n-1 号同学)。当他面朝内时,往右边传递3名同学,就会变成 0+3=3 号同学拥有礼物。如果0号同学往左边传递3名同学,就会变成 0-3=-3 号同学拥有礼物,显然没有-3号同学。考虑0号同学和7号同学等价(因为6号同学的下一个就是0号同学),1号同学和8号同学等价,……可以猜出:-3号同学和 -3+n=4号同学等价。面朝外的同学往右边数 y 个就是编号增加 y,往左边数就是编号减少 y。如果得到的编号不在 0~n-1 的范围内,则需要通过增减n调整到这个范围内。为了达到这个目的,可以使用取余数的方式。如果这名同学面朝外,那么方向和加减的关系就和上面一种情况反过来,但是依然需要调整到 0~n-1 的范围内。
枚举这4种情况,可以得到如下代码:
#include <iostream>
#include <string>
using namespace std;
const int MAXN = 1e6 + 5;
struct node { //使用结构体存储同学的姓名和方向
int head;
string name;
};
node a[MAXN];
int n, m, x, y;
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++)
cin >> a[i].head >> a[i].name;
int now = 0;
for (int i = 1; i <= m; i++) {
scanf("%d%d",&x,&y);
if (a[now].head == 0 && x == 0) //情况 1
now = (now + n - y) % n;
else if (a[now].head == 0 && x == 1) //情况2
now = (now + y) % n;
else if (a[now].head == 1 && x == 0) //情况3
now = (now + y) % n;
else if (a[now].head == 1 && x == 1) //情况4
now = (now + n - y) % n;
}
cout << a[now].name << endl;
return 0;
}
这段代码还能进行一些精简,例如将一些情况合并(提示:使用异或判断同学的朝向和传递方向甚至可以压缩成唯一的一种情况),但是这段示例代码便于读者理解。