2407: 【普及/提高-】【P1065】作业调度方案
题目描述
我们现在要利用 台机器加工 个工件,每个工件都有 道工序,每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。
每个工件的每个工序称为一个操作,我们用记号 j-k 表示一个操作,其中 为 到 中的某个数字,为工件号; 为 到 中的某个数字,为工序号,例如 2-4 表示第 个工件第 道工序的这个操作。在本题中,我们还给定对于各操作的一个安排顺序。
例如,当 时,1-1,1-2,2-1,3-1,3-2,2-2 就是一个给定的安排顺序,即先安排第 个工件的第 个工序,再安排第 个工件的第 个工序,然后再安排第 个工件的第 个工序,等等。
一方面,每个操作的安排都要满足以下的两个约束条件。
-
对同一个工件,每道工序必须在它前面的工序完成后才能开始;
-
同一时刻每一台机器至多只能加工一个工件。
另一方面,在安排后面的操作时,不能改动前面已安排的操作的工作状态。
由于同一工件都是按工序的顺序安排的,因此,只按原顺序给出工件号,仍可得到同样的安排顺序,于是,在输入数据中,我们将这个安排顺序简写为 1 1 2 3 3 2。
还要注意,“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时,有可能排在后面的某个操作比前面的某个操作先完成。
例如,取 ,已知数据如下(机器号/加工时间):
| 工件号 | 工序 | 工序 |
|---|---|---|
则对于安排顺序 1 1 2 3 3 2,下图中的两个实施方案都是正确的。但所需要的总时间分别是 与 。
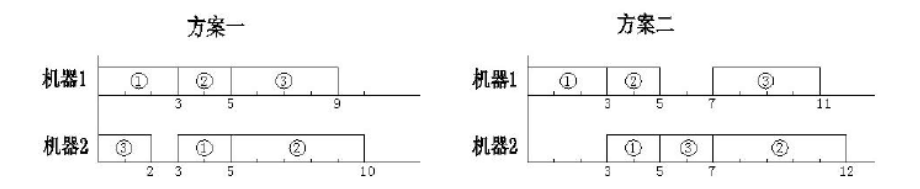
当一个操作插入到某台机器的某个空档时(机器上最后的尚未安排操作的部分也可以看作一个空档),可以靠前插入,也可以靠后或居中插入。为了使问题简单一些,我们约定:在保证约束条件()()的条件下,尽量靠前插入。并且,我们还约定,如果有多个空档可以插入,就在保证约束条件()()的条件下,插入到最前面的一个空档。于是,在这些约定下,上例中的方案一是正确的,而方案二是不正确的。
显然,在这些约定下,对于给定的安排顺序,符合该安排顺序的实施方案是唯一的,请你计算出该方案完成全部任务所需的总时间。
输入
第 行为两个正整数 , ,用一个空格隔开, (其中 表示机器数, 表示工件数)
第 行: 个用空格隔开的数,为给定的安排顺序。
接下来的 行,每行都是用空格隔开的 个正整数,每个数不超过 。
其中前 行依次表示每个工件的每个工序所使用的机器号,第 个数为第 个工序的机器号,第 个数为第 个工序机器号,等等。
后 行依次表示每个工件的每个工序的加工时间。
可以保证,以上各数据都是正确的,不必检验。
输出
样例输入 复制
2 3
1 1 2 3 3 2
1 2
1 2
2 1
3 2
2 5
2 4样例输出 复制
10提示
NOIP 2006 提高组 第三题
1.输入
2.遍历字符串,找到'-
3.判定是否需要展开
-左右同时为数字,或者左右同时为字母
-如果s[i+1]-s[i-1]==1,去掉'
剩下的所有情况,都保留"-
4.展开的规则
-如果p3是1,顺序展开
-如果p3是2,倒序展开
-如果p1是1,小写填充,如果是2,大写填充,如果是3,"*号填充
-每个字符输出p2次
#include<bits/stdc++.h>
using namespace std;
struct gongjian {
int jqh;
int sj;
}gj_sx[20][20];
int n,m,gj_gx[20],gj_last[20],apsx[400];
int jq_sj[20][8000] = {0};
void inits() {
cin >> m >> n;
for (int i = 0;i < m*n; i++) {
cin >> apsx[i];
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <=m; j++) {
cin >> gj_sx[i][j].jqh;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <=m; j++) {
cin >> gj_sx[i][j].sj;
}
}
for (int i = 1;i <= n; i++) {
gj_gx[i] = 1;
}
}
bool judge(int bgtime, int endtime, int jqh) {
for (int i = bgtime; i <= endtime; i++)
if (jq_sj[jqh][i] == 1) return false;
return true;
}
void chuli() {
for (int i = 0; i < m*n; i++) {
int gj = apsx[i];
int gx = gj_gx[gj]++;
int jqh = gj_sx[gj][gx].jqh;
int sj = gj_sx[gj][gx].sj;
int bgtime = gj_last[gj];
while(true) {
if (judge(bgtime+1,bgtime+sj,jqh)) {
for (int j = bgtime+1; j <= bgtime+sj; j++) {
jq_sj[jqh][j] = 1;
}
gj_last[gj] = bgtime+sj;
break;
}
bgtime++;
}
}
}
int main(){
inits();
chuli();
int max = gj_last[1];
for (int i = 1; i <=n ;i++) {
if (max < gj_last[i]) max = gj_last[i];
}
cout << max;
return 0;
}