3018: 【普及/提高-】【P1364】医院设置
内存限制:128 MB
时间限制:1.000 S
评测方式:文本比较
命题人:
提交:4
解决:4
题目描述
设有一棵二叉树,如图:
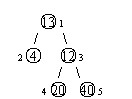
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为 。如上图中,若医院建在1 处,则距离和 ;若医院建在 处,则距离和 。
输入
第一行一个整数 ,表示树的结点数。
接下来的 行每行描述了一个结点的状况,包含三个整数 ,其中 为居民人口数, 为左链接(为 表示无链接), 为右链接(为 表示无链接)。
输出
一个整数,表示最小距离和。
样例输入 复制
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0样例输出 复制
81提示
数据规模与约定
对于 的数据,保证 ,,。
#include<bits/stdc++.h>
using namespace std;
struct node{
int left,right,father,value;
} t[105];
int n,sum, ans = INT_MAX, vis[105]={0};
void dfs(int step, int pos) {
sum +=step*t[pos].value;
int fa=t[pos].father,l=t[pos].left,r=t[pos].right;
if(fa && !vis[fa]) {
vis[fa]=1;
dfs(step+1,fa);
}
if(l && !vis[l]) {
vis[l]=1;
dfs(step+1,l);
}
if(r && !vis[r]) {
vis[r]=1;
dfs(step+1,r);
}
}
int main(){
cin >> n;
for (int i = 1 ;i <=n ; i++) {
cin >> t[i].value >> t[i].left >> t[i].right;
t[ t[i].left ].father=i;
t[ t[i].right ].father=i;
}
for (int i = 1;i <=n ;i++) {
sum=0;
memset(vis,0,sizeof(vis));
vis[i]=1;
dfs(0,i);
ans = min(ans,sum);
}
cout << ans;
return 0;
}
#include<bits/stdc++.h>
using namespace std;
struct node{
int left,right,father,value,step;
} t[105];
int n,sum, ans = INT_MAX, vis[105]={0};
void bfs(int k) {
queue<node> q;
node tn=t[k];
tn.step=0;
q.push(tn);
while(!q.empty()) {
tn=q.front();
q.pop();
sum +=tn.value*tn.step;
int fa=tn.father,l=tn.left,r=tn.right;
if(fa && !vis[fa]) {
vis[fa]=1;
node tn2=t[fa];
tn2.step=tn.step+1;
q.push(tn2);
}
if(l && !vis[l]) {
vis[l]=1;
node tn2=t[l];
tn2.step=tn.step+1;
q.push(tn2);
}
if(r && !vis[r]) {
vis[r]=1;
node tn2=t[r];
tn2.step=tn.step+1;
q.push(tn2);
}
}
}
int main(){
cin >> n;
for (int i = 1 ;i <=n ; i++) {
cin >> t[i].value >> t[i].left >> t[i].right;
t[ t[i].left ].father=i;
t[ t[i].right ].father=i;
}
for (int i = 1;i <=n ;i++) {
sum=0;
memset(vis,0,sizeof(vis));
vis[i]=1;
bfs(i);
ans = min(ans,sum);
}
cout << ans;
return 0;
}