3062: 【普及+/提高】【P2822】组合数问题
内存限制:512 MB
时间限制:2.000 S
评测方式:文本比较
命题人:
提交:11
解决:2
题目描述
组合数 $\binom{n}{m}$ 表示的是从 $n$ 个物品中选出 $m$ 个物品的方案数。举个例子,从 $(1,2,3)$ 三个物品中选择两个物品可以有 $(1,2),(1,3),(2,3)$ 这三种选择方法。根据组合数的定义,我们可以给出计算组合数 $\binom{n}{m}$ 的一般公式:
$$\binom{n}{m}=\frac{n!}{m!(n-m)!}$$
其中 $n!=1\times2\times\cdots\times n$;特别地,定义 $0!=1$。
小葱想知道如果给定 $n,m$ 和 $k$,对于所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 有多少对 $(i,j)$ 满足 $k|\binom{i}{j}$。
输入
第一行有两个整数 ,其中 代表该测试点总共有多少组测试数据, 的意义见问题描述。
接下来 行每行两个整数 ,其中 的意义见问题描述。
输出
共 行,每行一个整数代表所有的 中有多少对 满足 。
样例输入 复制
1 2
3 3样例输出 复制
1提示
【样例1说明】
在所有可能的情况中,只有 一种情况是 的倍数。
【子任务】
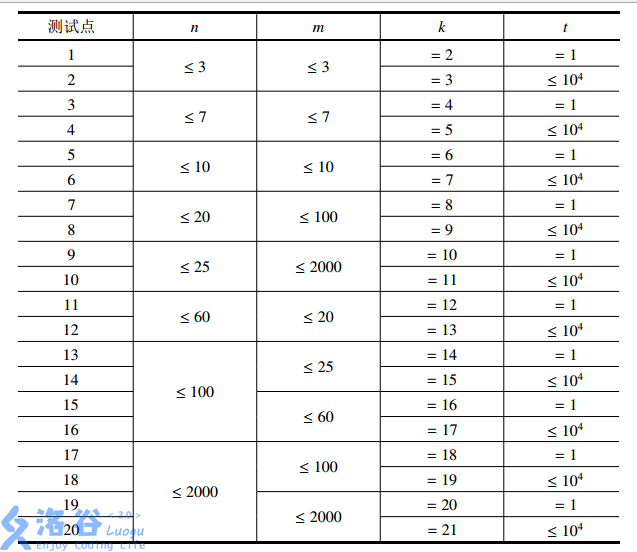
- 对于全部的测试点,保证 ,。

#include<bits/stdc++.h>
using namespace std;
const int N = 2010; //n的数值上限
long long C[N][N];
int main(){
int t,k,m,n;
cin>>t>>k;
for(int i=0;i< N;i++) {
C[i][0]=C[i][i]=1;
for(int j=1;j<i;j++)
C[i][j]=(C[i-1][j]+C[i-1][j-1])%k; //递推
}
while(t--) {
int ans=0;
cin>>n>>m;
for(int i=0;i<=n;i++)
for(int j=0;j<=min(i,m);j++)
ans+=C[i][j]==0;
cout<<ans<<endl;
}
return 0;
}

#include<bits/stdc++.h>
using namespace std;
const int N = 2010; //n的数值上限
int C[N][N];
int s[N][N]; //二维前缀和
int main(){
//默认初始值-1,之所以初始为-1,是怕默认的0无法描述是模完变成的0,还是天生默认就是0,-1就有这个好处。
memset(C, -1, sizeof C);
int t,k,m,n;
cin>>t>>k;
for(int i=0;i<N;i++) {
C[i][0]=C[i][i]=1;
for(int j=1;j<i;j++)
C[i][j]=(C[i-1][j]+C[i-1][j-1])%k; //递推
}
for (int i = 1; i < N; i++) //标准的二维前缀和
for (int j = 1; j < N; j++)
s[i][j] = (C[i][j] == 0 ? 1 : 0) + s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1];
while (t--) { //处理t次询问
cin >> n >> m;
cout << s[n][m] << endl;
}
return 0;
}