4147: 方格取数（number）

内存限制：512 MB 时间限制：1.000 S
评测方式：文本比较 命题人：
提交：6 解决：2

题目描述

设有 lns="http://www.w3.org/1998/Math/MathML">�×� 的方格图，每个方格中都有一个整数。现有一只小熊，想从图的左上角走到右下角，每一步只能向上、向下或向右走一格，并且不能重复经过已经走过的方格，也不能走出边界。小熊会取走所有经过的方格中的整数，求它能取到的整数之和的最大值。

输入

第一行有两个整数 lns="http://www.w3.org/1998/Math/MathML">�,�。

接下来 lns="http://www.w3.org/1998/Math/MathML">� 行每行 lns="http://www.w3.org/1998/Math/MathML">� 个整数，依次代表每个方格中的整数。

输出

一个整数，表示小熊能取到的整数之和的最大值。

样例输入 复制 

3 4
1 -1 3 2
2 -1 4 -1
-2 2 -3 -1

样例输出 复制 

9

提示

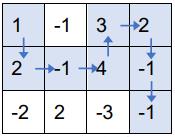
【样例 lns="http://www.w3.org/1998/Math/MathML">1 解释】

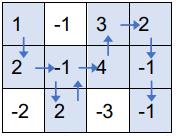
按上述走法，取到的数之和为 lns="http://www.w3.org/1998/Math/MathML">1+2+(−1)+4+3+2+(−1)+(−1)=9，可以证明为最大值。

注意，上述走法是错误的，因为第 lns="http://www.w3.org/1998/Math/MathML">2 行第 lns="http://www.w3.org/1998/Math/MathML">2 列的方格走过了两次，而根据题意，不能重复经过已经走过的方格。

另外，上述走法也是错误的，因为没有走到右下角的终点。

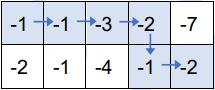
【样例 lns="http://www.w3.org/1998/Math/MathML">2 解释】

按上述走法，取到的数之和为 lns="http://www.w3.org/1998/Math/MathML">(−1)+(−1)+(−3)+(−2)+(−1)+(−2)=−10，可以证明为最大值。因此，请注意，取到的数之和的最大值也可能是负数。

【数据范围与提示】

  • 对于 lns="http://www.w3.org/1998/Math/MathML">20% 的数据，lns="http://www.w3.org/1998/Math/MathML">�,�≤5。
  • 对于 lns="http://www.w3.org/1998/Math/MathML">40% 的数据，lns="http://www.w3.org/1998/Math/MathML">�,�≤50。
  • 对于 lns="http://www.w3.org/1998/Math/MathML">70% 的数据，lns="http://www.w3.org/1998/Math/MathML">�,�≤300。
  • 对于 lns="http://www.w3.org/1998/Math/MathML">100% 的数据，lns="http://www.w3.org/1998/Math/MathML">1≤�,�≤103。方格中整数的绝对值不超过 lns="http://www.w3.org/1998/Math/MathML">104。 
  • #include<bits/stdc++.h>
using namespace std;
/* 
左上角走到右下角
每一步只能向上、向下或向右走一格
不能重复经过已经走过的方格

计算的结果，要用 long long
*/
const int N=1010;
int a[N][N]; //读入的每个点的值
typedef long long LL;
LL f[N][N];
int n,m;
int main(){
    scanf("%d%d",&n,&m);
    for(int i = 1;i<= n;i++){
        for(int j=1;j<= m;j++){
		    scanf("%d",&a[i][j]);
		}
	}
    /*
    DP 求出走到每个点经过的数字和的最大值
	一列一列求， 对于每一列而言，要求从上向下走到每个点经过的数字和的最大值
	也要求从下向上走到每个点经过的数字和的最大值
    */
    memset(f,-0x7f,sizeof(f));
    LL ma; //走到每个格子经过的数字和最大
    f[1][0]= 0;
	for(int j=1;j<= m;j++){ //从上向下求
        ma =-1e18;
        for(int i= 1;i<= n;i++){
            ma = max(ma,f[i][j-1])+ a[i][j];
            f[i][j]= max(f[i][j],ma);
        }
        //从下向上求
        ma =-1e18;
        for(int i=n;i>=1;i--) {
	        ma=max(ma,f[i][j-1])+a[i][j];
	        f[i][j]=max(f[i][j],ma);
        }
	}
    cout<<f[n][m];
    return 0;
}

来源/分类

提交提交记录统计露一手!