4190: 欧拉筛法

内存限制：128 MB 时间限制：1.000 S
评测方式：文本比较 命题人：
提交：1 解决：1

题目描述

        埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。如：30=2*3*5，使用埃氏筛法会被2的倍数时标记一次，3的倍数时标记一次，5的倍数时标记一次，造成效率达不到最优，而欧拉筛法改进这个不足。

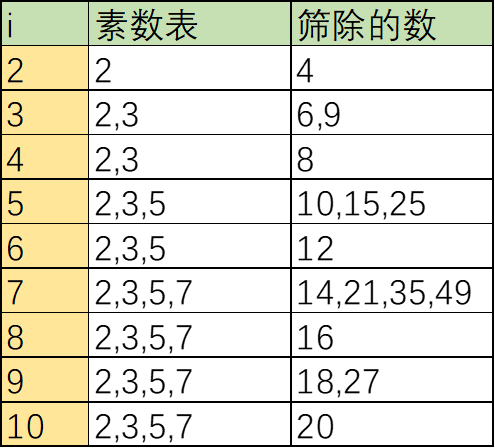
    给定一个大于2的偶数，在所有满足“任意一个大于2的偶数可以由两个质数相加得到”这个特点的质数对中，找出两个质数差值最小的一对，并将差值输出（差值为大数减小数的值，两个质数相等时差值为0）。

    例如：偶数16，满足特点的质数对有（5，11）和（3，13），差值最小的一对是（5，11），11减5，差值为6


样例输入 复制 

16

样例输出 复制 

6

提示

n=int(input())
a=[1]*(n+1) #全部初始化为素数
ls=[] #存放已筛选的素数
for i in range(2,n+1):
    if a[i]==1: 
        ls.append(i)
    for prime in ls:
        if i*prime>n:break
        a[i*prime] = 0            
        if i%prime == 0:break
for i in range(n//2,n+1): 
    if i in ls and n-i in ls:
        print(i+i-n)
        break

来源/分类

提交提交记录统计露一手!