4251: 花卉摆放
内存限制:128 MB
时间限制:1.000 S
评测方式:文本比较
命题人:
提交:1
解决:1
题目描述
六月一日是国际儿童节,小蓝的学校为迎接儿童节要在学校的一块正方形空地上使用不同颜色的花卉摆放图案。为了摆放的更精准,图案更漂亮,小蓝把这块正方形空地同比例缩小将其画在纸上,并平分成100*100的方格,每个方格的坐标点为(1,1)...... (100,100),如下图:
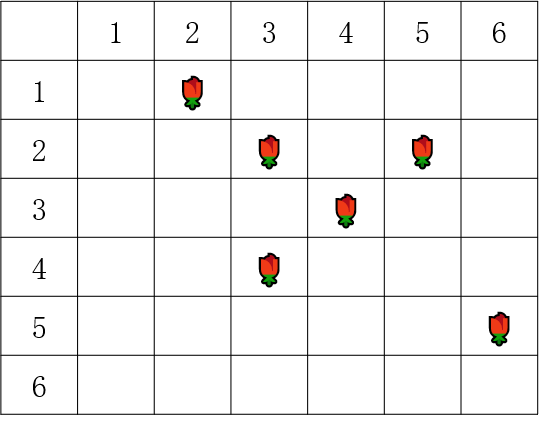
首先在指定坐标的方格内放置红色的花卉(每个方格放一盆),完成后,找出最多有多少盆红色花卉在同一条直线上。(同一直线包含同一列、同一行、同一对角线,红色花卉可以连续也可以不连续)
如:随机指定坐标(1,2)、(2,3)、(2,5)、(3,4)、 (4,3)、(5,6)的方格内放置红色的花卉,其中最多的红色花卉在同一条直线上的坐标点为(1,2)、(2,3)、(3,4)、(5,6),故最多有4盆红色的花卉在同一条直线上。
输入
输入n对正整数,每一对正整数之间以一个空格隔开,代表放置红色花卉的方格位置。每对正整数中的两个数字以英文逗号隔开。
输出
输出最多有多少盆红色花卉在同一条直线上。
样例输入 复制
1,2 2,3 2,5 3,4 4,3 5,6
样例输出 复制
4提示
算法分析:
1.首先把每个位置的坐标读入列表ls中
2.然后遍历列表的坐标,把行坐标相同的位置更新到行坐标为键值的字典中,列坐标做相同的处理
3.斜线做类似的处理,具体方法后面详解
4.找出四个字典中各自的最大值
在四个最大值中找最大值,即为答案
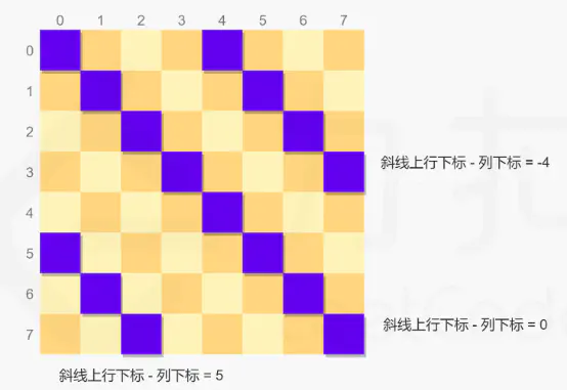
左斜线:左斜线为从左上到右下方向,同一左斜线上的每个位置满足行下标与列下标之差相等,例如(1,1)和(3,3)在同一条左斜线上,行下标-列下标=0;例如(1,5)和(2,6)在同一条左斜线上,行下标-列下标=-4;
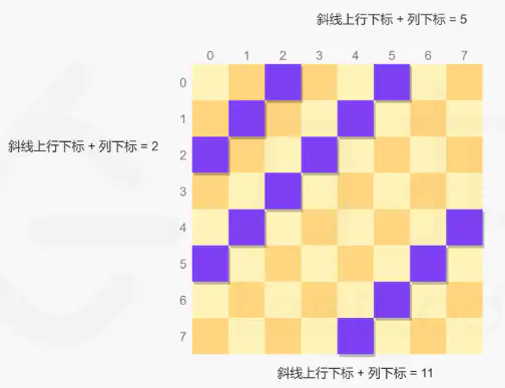
右斜线:右斜线为从右上到左下方向,同一右斜线上的每个位置满足行下标与列下标之和相等,例如(2,0)和(1,1)在同一条右斜线上,行下标+列下标=2;例如(1,4)和(2,3)在同一条右斜线上,行下标+列下标=5;
li=list(input().split(' '))
ls=[]
for i in li:
temp=[]
for j in i.split(','):
temp.append(int(j))
ls.append(temp)
maxL=0
dI={}
dJ={}
dLX={}
dRX={}
for v in ls:
i=v[0]
j=v[1]
lx=i-j
rx=i+j
dI[i]=dI.get(i,0)+1
dJ[j]=dJ.get(j,0)+1
dLX[lx]=dLX.get(lx,0)+1
dRX[rx]=dRX.get(rx,0)+1
maxL=max(maxL,max(dI.values()))
maxL=max(maxL,max(dJ.values()))
maxL=max(maxL,max(dLX.values()))
maxL=max(maxL,max(dRX.values()))
print(maxL)