4252: 杨辉三角

内存限制：128 MB 时间限制：1.000 S
评测方式：文本比较 命题人：
提交：1 解决：1

题目描述

        杨辉三角形 ，是二项式系数在三角形中的一种几何排列。中国南宋数学家杨辉在 1261 年所著的 《详解九章算法》—书有明确记载。欧洲数学家帕斯卡在 1654 年发现这一规律 ，所以又叫做帕斯卡三角形。其定义为其顶端（第 1行）是 1；第 2 行是两个 1；第 3 行是'1，2，1'，中间的”2”是其上方相邻的两个数字的和;依次类推 ，产生如图所示的杨辉三角形。 

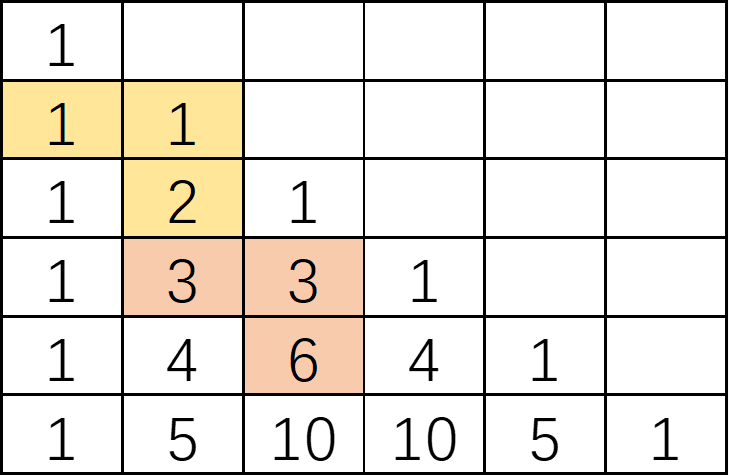
    对于任意输入的3~15之间的正整数n，请编程输出前n行数字、以及由其组成的杨辉三角形。

函数提示∶print('{∶<3}'.format(10))能够以3个字符宽度左对齐的方式显示数字10。

                                                                          

输入

一个正整数n（3≤n≤15）

输出

由两部分组成。

第一部分输出由n行数字组成的列表；

第二部分输出n行数字组成的杨辉三角形。具体输出格式参考如下样例。

样例输入 复制 

6

样例输出 复制 

[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1] 
                    1       
                1       1       
            1       2       1       
        1       3       3       1       
    1       4       6       4       1       
1       5       10      10      5       1

提示

n=int(input())
a=[[0]*n for _ in range(n)]  #初始化所有数为0
for i in range(n):  #初始化第1列和对角线为1
    a[i][0]=a[i][i]=1
for i in range(2,n):  #从第3行第2列开始填充数值
    for j in range(1,i):
        a[i][j]=a[i-1][j]+a[i-1][j-1]
for i in range(n):  #删除数值依然为0的元素
    for j in range(n-1,-1,-1):
        if (a[i][j]==0):
            a[i].pop(j)
for r in a:
    print(r)
m=1
for r in a:
    for j in range(n-m):
        #引号里是4个空格
        print('{:<4}'.format('  '),end='')
    for j in a[m-1]:
        print('{:<4}'.format(j),end='')
        #引号里是4个空格
        print('{:<4}'.format('  '),end='')  
    print()
    m+=1

来源/分类

提交提交记录统计露一手!